A Closer Look at The Heinrich Accident Triangle and how it works

Average Reading Time is 7 minutes

When investigating a worksite, employers and workers are tasked to identify hazards in their operations and shortcomings in their safety and health programs. Most importantly, employers and workers are required to identify and implement the corrective actions necessary to prevent future incidents. It is important that delegates are aware of the various analysis methods available which they can tap on to identify these worksite incidents. We’ll cover one of the many incident investigation techniques – the Heinrich Accident Triangle and how it works.

What is the Heinrich Accident Triangle?

 

 

 

 

 

 

 

 

 

 

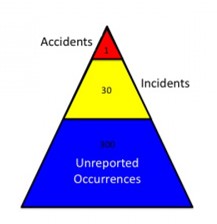
The Heinrich Accident Triangle which is also known as the Bird’s triangle or accident triangle, is a theory of industrial accident prevention. It shows a relationship between serious accidents, minor accidents and near misses and proposes that if the number of minor accidents is reduced then there will be a corresponding fall in the number of serious accidents. First coined by Herbert William Heinrich in 1931, the Heinrich Triangle has since been updated and expanded upon by others such as Frank E. Bird.  

The Heinrich’s law was based on probability and assumes that the number of accidents is inversely proportional to the severity of those accidents. As such using the Heinrich Accident Triangle theory, it suggested that 88% of all accidents were caused by a human decision to carry out an unsafe act.

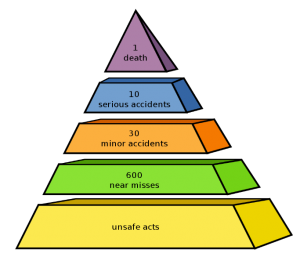
The theory was developed further by Frank E Bird in 1966 based on the analysis of 1.7 million accident reports from almost 300 companies. He produced an amended triangle that showed a relationship of one serious injury accident to 10 minor injury (first aid only) accidents, to 30 damage causing accidents, to 600 near misses. Bird showed a relationship between the number of reported near misses and the number of major accidents and claimed that most of these accidents could be predicted and prevented by an appropriate intervention.

In referring to the ratio detailed in the above triangle, Bird’s Triangle, it should be remembered that this represents accidents reported and incidents discussed with the individuals and not the total number of accidents or incidents that actually occurred but went unreported.

How to use the Accident triangle?

Regardless of the triangle used (be it Bird’s Triangle or Heinrich’s traditional triangle) the hypothesis for both triangles are fundamentally the same. They both leverage on the hypothesis that rather than focus on the few injuries at the top of the triangle, companies should to learn how to avoid accidents at the bottom or base of the triangle. This is because the accidents at the base of the pyramid could be major and catastrophic losses.

The main use of these triangles is to convey the message that serious outcome accidents tend to happened rarely and randomly. As such they are notoriously difficult to predict. Near misses/incidents, on the other hand, happen far more frequently. Many near misses will be minor events of little or no consequences; if they happen again there would be no serous outcome. but some near misses will have the potential for very serious injury. These near misses should be thoroughly investigated, and preventive measures put in place to avoid the recurrence.

Limitations of the triangle

So, with all the above theories and explanations behind how the triangle works, there are certain limitations that the triangle has too. The following lists three of the limitations that the accident triangle experiences

• Hard to verify the statistics
• Dataset might be skewed
• About actual event outcomes

Hard to verify statistics

Firstly, the statistics on which Heinrich based his theory are hard to verify now. Bird’s statistics are based on insurance statistics available in the 1960s. Hence the ratio of near misses to serious accidents would only be indicative at best today.

However, even if the statistics were valid, the triangle assumes that an individual organisation’s datasets are complete, which is only true in some cases. In other words, serious incidents will almost certainly be known, but perhaps not all minor injuries will be recorded. This is because the complete transparency of all near misses cannot be assumed.

Datasets might be skewed

Secondly, datasets can also be skewed by the fact that not all near misses or unsafe acts are of the same gravity. To illustrate the point, in an individual case, if an accident had occurred — rather than the reported near miss — would the outcome have been a minor accident, a RIDDOR-reportable incident or perhaps even a fatality? Bird’s triangle’s theory assumes that people lump all near misses together, regardless of possible outcome. Although sometimes, it is indeed difficult to tell how serious a near miss could have been, especially if the near miss triggered a chain of events that led to a serious incident. This domino effect of failures is the so-called “Swiss cheese” event which, again, Bird’s Triangle doesn’t overtly consider.

About Actual Event Outcomes

Thirdly, Bird’s Triangle is about actual event outcomes. It doesn’t particularly consider risk potential. For example, the possibility of certain serious incidents occurring may not necessarily be indicated by a higher volume of near misses. Equally, reducing the number of minor incidents doesn’t necessarily, in practice, reduce fatalities.

If you want to find out more about incident investigation, do read our other blogs below and our course on Incident Investigation.